참고 자료: Cyrill Stachniss 교수님의 Robot Mapping 강의
http://norman3.github.io/prml/docs/chapter02/3_1.html
아주 오래전부터 공부하려고 했었던 Robot Mapping 강의를 들으면서 그 내용을 정리하여 기록해두고자 합니다. 이 강의는 robot mapping (SLAM)에 관한 SOTA system의 내용들 (Kalman filter, EKF, UKF, Particle filter, Graph-based Approach...) 을 다루고 있기 때문에 SLAM에 관한 기초를 공부하기에 좋은 자료라고 생각 됩니다.
이번 글에서는 Bayes-filter의 한 종류이면서 가장 빈번하게 사용되고 있는 Kalman filter와 Extended Kalman filter에 대해 알아 보도록 하겠습니다.
Kalman Filter란?
1950년대 후반에 루돌프 칼만( Rudolf E. Kalman)에 의해서 개발되었으며 시스템의 확률분포가 Gaussian 이고, 시스템이 선형 이라는 가정/조건 하에서는 optimal solution 기법이다.
이전글에서 현재 상태를 예측하기 위한 bayes filter의 prediction step과 correction step은 다음과 같음을 보였다.

이때, prediction step과 correction step의 motion model과 observation model을 올바르게 추정할 수 있다면, $bel(x_{t-1})$의 값은 알고 있는 값이기 때문에 다음 상태($bel(x_t)$)에대한 추정을 할 수 있다. 이번 글에서 이러한 motion model과 observation model을 알아내는 한 방법인 kalman filter대해서 알아볼 것이다.
그 전에 kalman filter는 시스템의 특징이 Gaussian 확률분포를 가질때만 적용할 수 있기 때문에 먼저 Gaussian 확률분포가 무엇인지 짧게 확인하고 넘어가도록 하겠다.
가우시안 확률분포의 식은 다음과 같다.
$p(x)\ =\ det(2\pi\sum)^{-\frac{1}{2}}\ exp(-\frac{1}{2}(x\ -\ \mu)^{T}\sum^{-1}(x\ -\ \mu))$
여기서 $\mu$는 Gaussian distribution의 평균이고, $\sum$은 covariance를 나타낸다. 이때 가우시안 확률분포의 중요한 특징으로 다음의 marginalization과 conditioning이 모두 gaussian 확률 분포를 가진다. (norman3님 블로그참고)
$x\ = \ \begin{pmatrix}x_a\\x_b\end{pmatrix},\ \ \ p(x)\ =\ \aleph$ 일때,
- Marginalization: $p(x_a)\ =\ \aleph,\ \ \ p(x_b)\ =\ \aleph$
- Conditioning: $p(x_a|x_b)\ =\ \aleph,.\ \ \ p(x_b|x_a)\ =\ \aleph$
이러한 conditioning 특징 덕분에 prediction step 과 correction step에서 $p(x_t\ |\ x_{t-1},\ u_t)$와 $p(z_t\ |\ x_t)$를 계산해도 gaussian 분포의 특징이 유지된다. 또 marginalization 특징으로 인해서 $p(z_t\ |\ x_t)*\overline{bel}(x_t)$과 같은 gaussian 확률 분포끼리의 곱셈을 하여도 역시 gaussian이라는 특성이 유지된다.
Kalman Filter
이제 이러한 특징을 바탕으로 bayes-filter의 한 종류인 Kalman filter에 대해서 공부해 보도록 하겠다. 앞에서도 말했던 것처럼 kalman filter는 linear model을 조건으로 한다. 이에 따라서 motion model과, observation model의 식은 다음과 같이 선형 방정식으로 포현된다.
Motion model: $x_t\ =\ A_tx_{t-1}+B_tu_t+\epsilon_t \longrightarrow$ 이전 state와 command가 있을 때 다음의 motion을 예측
Observation model: $z_t\ =\ C_tx_t+\delta_t \longrightarrow$ 현재 state를 알 때 관측되어야 할 값을 예측, 예를들어 내가 특정 위치에 있고 이 위치에서는 5m앞에 벽이 있다는것을 알 때, 나의 관측값이 5m가 나올 것이라고 예측하는 것.
이때, 가우시안 확률분포의 식으로부터 Motion model $p(x_t\ |\ u_t, x_{t-1})$은 앞에서 표현한 선형방정식에 의해 다음과 같이 나타낼 수 있다.
$p(x_t\ |\ u_t,\ x_{t-1})\ =\ det(2\pi R_t)^{-\frac{1}{2}}\ exp(-\frac{1}{2}(x_t\ -\ A_t x_{t-1}\ -\ B_t u_t)^{T}R_t^{-1}(x_t\ -\ A_t x_{t-1}\ -\ B_t u_t))$
이어서 observation model $p(z_t\ |\ x_t)$ 또한 다음과 같다.
$p(z_t\ |\ x_t)\ =\ det(2\pi Q_t)^{-\frac{1}{2}}\ exp(-\frac{1}{2}(z_t\ -\ C_t x_t)^{T}Q_t^{-1}(z_t\ -\ C_t x_t))$
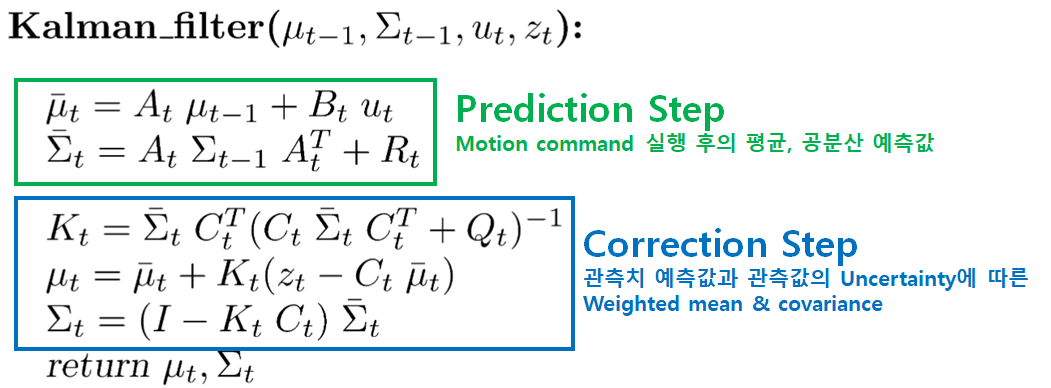
이를 바탕으로 전개되는 kalman filter의 수식은 다음과 같다.
'Robotics > SLAM' 카테고리의 다른 글
| [SLAM-Course] EKF SLAM (Extended Kalman Filter SLAM) - 07 (0) | 2020.06.30 |
|---|---|
| [SLAM-Course] Bayes Filter-05 (0) | 2020.06.23 |
| [SLAM-Course] Bayes Filter-04 (0) | 2020.06.21 |
| [SLAM-Course] Homogeneous Coordinates-03 (0) | 2020.06.20 |
| [SLAM-Course] SLAM 이란? (Introduction to Robot Mapping)-02 (0) | 2020.06.18 |



