참고 자료: Cyrill Stachniss 교수님의 Robot Mapping 강의
아주 오래전부터 공부하려고 했었던 Robot Mapping 강의를 들으면서 그 내용을 정리하여 기록해두고자 합니다. 이 강의는 robot mapping (SLAM)에 관한 SOTA system의 내용들 (Kalman filter, EKF, UKF, Particle filter, Graph-based Approach...) 을 다루고 있기 때문에 SLAM에 관한 기초를 공부하기에 좋은 자료라고 생각 됩니다.
SLAM을 하는 방식에는 여러가지 방법이 있는데 이중에서 다음의 3가지 방법에 대해서 배울 것이다.
- Kalman filter family
- Praticle filter
- Graph-based optimization approach
이전글에서 다루었던 Extended Kalman Filter(EKF)에 이어서 이번 글에서는 EKF의 개념을 SLAM에 어떻게 활용하는지 배운다. 이를 통해서 로봇의 위치를 추정하고 landmark의 지도를 그릴 수 있다.
EKF는 bayes filter의 prediction step과 correction step를 반복적으로 수행하면서 추정을하는 'recursive bayes filter' 이다.

Prediction step에서는 다음 상태를 추정하는데, 로봇의 위치를 추정하는 것과 더불어 landmark의 위치 또한 추정한다. 하지만 prediction step에서는 제어명령을 받은 후 한스텝 움직였을 때 로봇의 위치와 landmark의 위치를 추정하는 것이므로 일반적으로 (로봇이 부딪혀서 landmark의 위치가 변경되거나 없어지지 않는 다고 가정) 추정된 상태에서의 landmark의 위치는 변하지 않는다.
Correction step에서는 sensor로부터 측정된 값과 로봇의 운동모델에 따라 예측된 값의 차이를 바탕으로 state를 correction하고 update한다.
EKF SLAM
Kalman Filter Equation
아래 칼만필터의 수식을 나타내었다. 이번 글을 통해 수식의 2번부터 6번까지 어떻게 전개 되는지 살펴보도록 한다.

Filter Cycle
아래 정리된 cycle에서 1은 prediction step에 해당하고 2~4는 correction step을 위한 sub-step, 그리고 5가 correction step에 해당한다.
- State prediction: 제어명령을 받아 이동한 로봇의 새로운 위치를 추정 ($\mu_0, \sum_0, g(), G_t$)
- Measurement prediction: 새로운 로봇의 위치에서 관측될 것으로 예상되는 랜드마크의 위치 추정 ($H_t, h()$)
- Measurement: 센서로 부터 들어오는 랜드마크의 위치 관측 (Z_t)
- Data association: 현재 관측된 랜드마크가 실제 맵에서 어디에 위치해 있는지 아는 것.
- Update: 예측한 랜드마크 위치와 센서에서 관측된 랜드마크 위치의 차이 계산을 통한 state update ($\mu_1, \sum_1$)
- $\mu_1, \sum_1$을 이전값으로 하여 1~5 반복
이제 이를 표현이 비교적 간단한 2D case에 대해서 step별로 살펴보고 이를 3D문제로 확장하기로 한다. 2D case 이므로 로봇의 위치를 나타내는 state는 $(x, y, \theta)$ 이다.
State representation
n개의 landmark가 관측된다고 할 때, 예측할 state는 로봇의 state $(x, y, \theta)$ + 랜드마크 (x, y) 좌표 => 3+2n개가 된다. 이를 state vector와 covariance matrix 식으로 나타내면 다음과 같다.

$(x, y, \theta)$ : 로봇의 위치
$(m_{n,x}, m_{n,y})$ : 랜드마크의 위치
$(\sigma_{xx}, \sigma_{yy}, \sigma_{\theta\theta}, ...)$ : 로봇 위치의 covariance matrix
$(\sigma_{m,m})$ : 랜드마크들의 uncertainty와 랜드마크끼리의 correlation matrix
$(\sigma_{m,x}, \sigma_{x,m}...)$ : 랜드마크와 로봇의 위치간의 correlation matrix
이를 간단하게 다음과 같이 표현하기도 한다.


Initialization
위에서 정의된 state vector와 covariance는 다음과 같이 초기화 할 수 있다.
- 초기정보가 없으므로 로봇의 Initial 위치는 0으로 (Initial pose = 0)
- 마찬가지로 초기정보가 없기 대문에 correlation 값은 모두 0으로 (No info -> No correlation)
- 마지막으로 Landmark에 대한 초기 정보 또한 없기 때문에 Uncertainty는 $\infty$ (No info -> infinite uncertainty)
$\mu_0\ =\ \begin{pmatrix}0&0&0&\cdots&0\end{pmatrix}^T$
$\sum_0\ =\ \begin{pmatrix}0&0&0&0&\cdots&0\\0&0&0&0&\cdots&0\\0&0&0&0&\cdots&0\\0&0&0&\infty&\cdots&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&0&\cdots&\infty\end{pmatrix}$
State Prediction
현재 위치를 알고, 제어명령이 들어 왔을 때, 한스텝 이동한 후의 위치를 추정하는 것. 이때는 제어명령 $u_t$(motion command)에 따라 로봇만 이동하므로 랜드마크의 위치는 바뀌지 않는다. (충돌, 부서짐 등으로 인해 랜드마크가 변형되는 경우 제외)

변하는 것은, 로봇의 위치, 로봇의 uncertainty, 로봇과 랜드마크 사이의 correlation 이다. 그러므로 모든 요소에 대해 계산할 필요 없이 랜드마크의 수 만큼만 새로계산하면 되므로 비교적 computing cost가 적은 작업이다. 이때 위의 그림에서 붉은 색으로 표시된 예측한 pose의 uncertainty가 커지는 것을 볼 수 있는데 이는 아래 Motion model 식에서 처럼 $\epsilon_t$라는 노이즈가 추가 되었기 때문이다.
$x_t = A_t\ X_{t-1}\ +\ B_t\ u_t\ +\ \epsilon_t$
State Prediction은 EKF식에서 2번 3번에 해당하는 부분이다. 즉, $\overline{\mu_t},\ \overline{\sum_t}$를 구한다. 이때 $\mu_t, \sum_{t-1}$는 이전step의 계산을 통해 알고있는 값이고, $R_t$는 motion model의 uncertainty이므로 또한 알고있는 값이다. 그러므로 motion model에 관한 함수 $g()$와 motion model의 jacobian인 $G_t$만 구하면 된다.
1. $g(u_t,\ x_t)$ 계산
2D plane에서 움직이는 물체의 motion은 다음의 식으로 나타낼 수 있다.
$\begin{pmatrix}x'\\y'\\\theta'\end{pmatrix}\ =\ \begin{pmatrix}x\\y\\\theta\end{pmatrix}\ +\ \begin{pmatrix}-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\\frac{v_t}{\omega_t}cos\theta-\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\\omega_t\Delta t\end{pmatrix}$
이때 로봇에 입력되는 제어명령을 통해서는 랜드마크의 위치는 바뀌지 않으므로 위의 식은 다음과 같은 full state 식으로 나타낼 수 있다.
$\begin{pmatrix}x'\\y'\\\theta'\end{pmatrix}\ =\ \underbrace{\begin{pmatrix}x\\y\\\theta\end{pmatrix}\ +\begin{pmatrix}1&0&0&0\ldots0\\0&1&0&0\ldots0\\0&0&1&\underbrace{0\ldots0}_{2Ncols}\\\end{pmatrix}^T\ \begin{pmatrix}-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\\frac{v_t}{\omega_t}cos\theta-\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\\omega_t\Delta t\end{pmatrix}}_{g(u_t,x_t)}$
2. $G_t$ 계산
prediction step에서 update되는 것은 제어명령을 통해 이동한 로봇의 state만 해당 되므로 $G_t$는 다음과 같이 나타낼 수 있다.

이를 정리하면, 2D 예시에서 Motion model의 Jacobian matrix는 다음과 같다.
$\begin{matrix}G_t^x&=&\frac{\partial}{\partial(x,y,\theta)^T}\begin{bmatrix}\begin{pmatrix}x\\y\\\theta\end{pmatrix}+\begin{pmatrix}-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\\frac{v_t}{\omega_t}cos\theta-\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\\omega_t\Delta t\end{pmatrix}\end{bmatrix}\\\ &=&I+\frac{\partial}{\partial(x,y,\theta)^T}\begin{pmatrix}-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\\frac{v_t}{\omega_t}cos\theta-\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\\omega_t\Delta t\end{pmatrix}\\\ &=&I+\begin{pmatrix}0&0&-\frac{v_t}{\omega_t}cos\theta+\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\0&0&-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\0&0&0\end{pmatrix}\\\ &=&\ \begin{pmatrix}1&0&-\frac{v_t}{\omega_t}cos\theta+\frac{v_t}{\omega_t}cos(\theta+\omega_t\Delta t)\\0&1&-\frac{v_t}{\omega_t}sin\theta+\frac{v_t}{\omega_t}sin(\theta+\omega_t\Delta t)\\0&0&1\end{pmatrix}\end{matrix}$
이때, 3번 식으로부터 $\bar{\sum}_t\ =\ G_t\sum_{t-1}G_t^T\ +\ R_t$ 이므로 다음과 같다.

이로부터 matrix에서 state와 관련된 부분만 update되는 것을 확인할 수 있다.
Measurement Prediction
현재 state의 'best estimate' 를 가지고 내가 관측해야 할 값을 예측하는 것 - 다시말해, 주어진 state에서 어떤값이 관측될지 observation model의 식을 통해 예측하는 것.
$z_t = C_t\ x_t\ +\ \delta_t$
이번 step에서는 observation model 함수 $h()$를 구하고 이를 바탕으로 kalman gain계산을 위한 $h()$의 Jacobian matrix $H_t$를 구한다.
1. $h(\bar{\mu}_t)$ 계산
laser scanner와 같은 range-bearing sensor를 예로 들어본다. laser scanner는 laser beam을 쏘아서 물체에 반사되어 들어오는 값을 측정하고 이 값은 현재위치에서 해당 물체까지의 거리와 각도에 해당한다. $z_t^i\ =\ (r_t^i,\ \phi_t^i)^T$ 그러므로 반사된 물체가 landmark라고 한다면, landmark의 위치는 다음의 식으로 알 수 있다.
$\begin{pmatrix}\bar{\mu}_{j,x}\\\bar{\mu}_{j,y}\end{pmatrix}\ =\ \begin{pmatrix}\bar{\mu}_{t,x}\\\bar{\mu}_{t,y}\end{pmatrix}\ +\ \begin{pmatrix}r_t^i\ cos(\phi_t^i+\bar{\mu}_{t,\theta})\\r_t^i\ sin(\phi_t^i+\bar{\mu}_{t,\theta})\end{pmatrix}$
robot의 현재 위치와 랜드마크의 위치를 알고 있을 때 observation model은 다음과 같이 구성된다.
$\delta = \begin{pmatrix}\delta_x\\\delta_y\end{pmatrix}\ =\ \begin{pmatrix}\bar{\mu}_{j,x}-\bar{\mu}_{t,x}\\\bar{\mu}_{j,y}-\bar{\mu}_{t,y}\end{pmatrix}$
$q\ =\ \delta^T\ \delta$
$\hat{z}_t^i\ =\ h(\bar{\mu}_t)\ =\ \begin{pmatrix}\sqrt{q}\\atan2(\delta_y,\delta_x)-\bar{\mu}_{t,\theta}\end{pmatrix}$
이 식에서 $\sqrt{q}$는 로봇과 랜드마크의 euclidean 거리이며, 아래 행은 로봇과 랜드마크가 이루는 각도를 의미한다. 식으로부터 $h()$는 비선형 observation model이고 이를 linearize 하는 Jacobian matrix를 계산한다.
2. $H_t$ 계산
observation model의 Jacobian은 다음과 같다.
$H_t^i\ =\ \frac{\partial h(\bar{\mu}_t)}{\partial\bar{\mu}_t}$
그런데 이때 total state의 수는 (3+2n)개 이므로 이를 모든 state에 대해서 편미분 하면 jacobian matrix가 매우 커진다. 생각해보면 jacobian matrix는 robot의 현재 pose와 현재 landmark의 pose를 제외한 값들은 모두 0가 되므로 (현재 고려하는 값이 아닌 것은 어차피 관련없는 상수로 취급되어 미분하면 0이 된다.) $(x,y,\theta,m_{j,x},m_{j,y})$만을 고려한 2X5 크기의 행렬 $^{low}H_t^i$ 를 구하고 이를 확장하여 2X(3+2n) 행렬로 만든다.
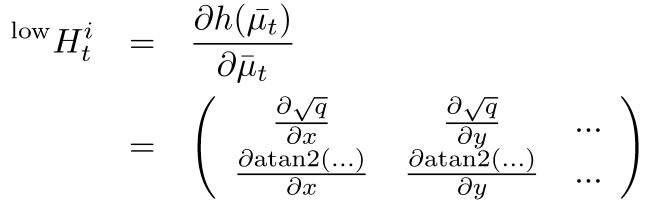

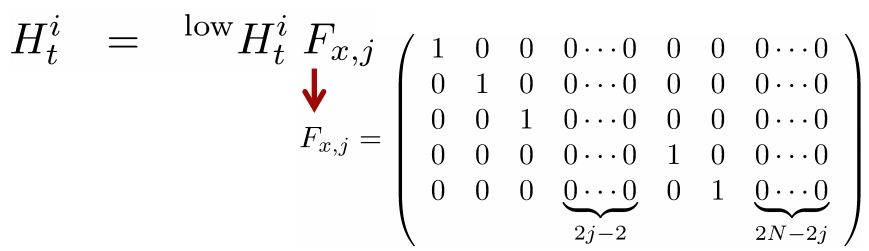
이를통해 $h(\bar{\mu}_t)\ 와\ H_t$를 구했으므로 다음은 Kalman filter의 식에 따라 순차적으로 해결할 수 있다.
Obtained Measurement
로봇에 장착된 센서로부터 들어오는 실제 센서 데이터 관측 값. 5번식의 $z_t$
Compute Difference Between h(x) and z
센서 관측값과, 관측값 예측치 사이의 차이 계산 5번식,6번식 계산 가능.

Update step
평균과 covariance 값을 update 한다. 아래 그림에서 처럼 모든 요소를 update해야 한다. 이때 계산해야 할 양은 quadratic complexity가 되고 kalman gain 식에 inverse가 있으므로 cubic complexity가 되므로 매우 computing cost가 높다.

'SLAM' 카테고리의 다른 글
| [SLAM-Course] Kalman Filter-06 (0) | 2020.06.24 |
|---|---|
| [SLAM-Course] Bayes Filter-05 (0) | 2020.06.23 |
| [SLAM-Course] Bayes Filter-04 (0) | 2020.06.21 |
| [SLAM-Course] Homogeneous Coordinates-03 (0) | 2020.06.20 |
| [SLAM-Course] SLAM 이란? (Introduction to Robot Mapping)-02 (0) | 2020.06.18 |




댓글